LOADING

加载过慢请开启缓存 浏览器默认开启

在深度神经网络中常用的激活函数及其性质

2025/2/26 深度学习 深度学习

1. 前言

在神经网络中，激活函数（Activation Function）是决定神经元输出信号的关键组件。它通过引入非线性特性，使神经网络能够学习和模拟复杂的模式。

激活函数的作用:

  1. 引入非线性：神经网络的作用便是用于拟合难以描述的函数关系，如果没有激活函数，多层神经网络等价于单层现性变换，无法解决非线性问题，即无法拟合出非线性函数关系。

  2. 控制输出范围：比如 Sigmoid 将输出压缩到 (0, 1)，适合概率输出

  3. 梯度传播：激活函数的导数影响反向传播的梯度，避免梯度消失或爆炸。

2. Sigmoid（Logistic 函数）

  • 公式： σ(x)=11+e−x\sigma(x) = \frac{1}{1 + e^{-x}}

  • 图像：S 型曲线，输出范围为 (0, 1)。（如下所示）

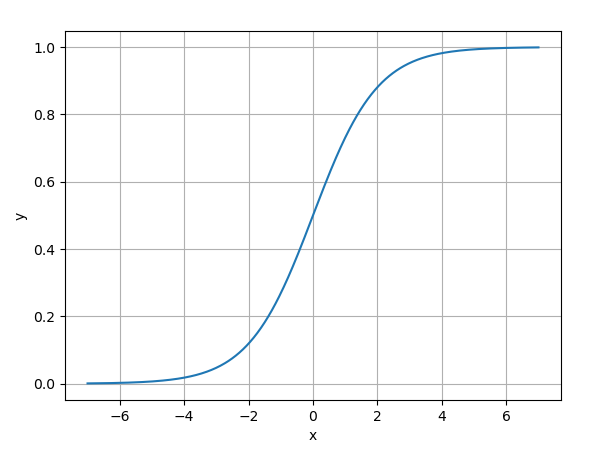
sigmoid

  • 优点：

    • 输出可解释为概率。
    • 平滑梯度，适合浅层网络。（深层网络不太适用）

  • 缺点：

    • 梯度消失：当输入绝对值较大时，导数接近 0 。
    • 非零中心化：输出均值不为 0，影响梯度更新效率。

  • 适用场景：二分类输出层、早期简单神经网络

3. Tanh（双曲正切函数）

  • 公式： tanh(x)=ex−e−xex+e−xtanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

  • 图像：S 型曲线，输出范围 (-1, 1)。（如下所示）

tanh

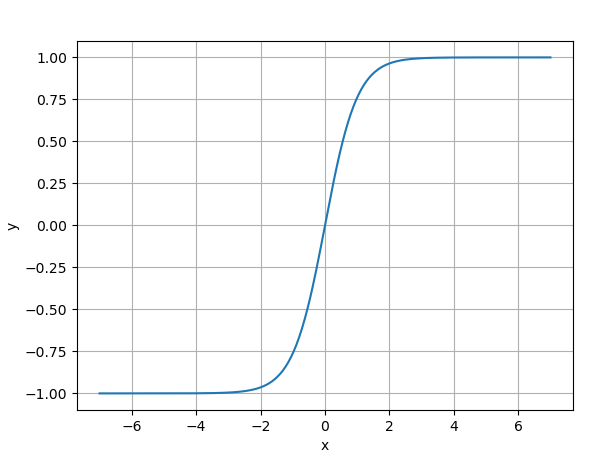
  • 优点：
    • 零中心化：输出均值为 0, 梯度更新更高效。
    • 比 Sigmoid 更陡峭的梯度。
  • 缺点：
    • 仍存在梯度消失问题。
  • 适用场景：隐藏层，尤其是 RNN、LSTM 等。

4. ReLU（Rectified Linear Unit 非线性激活单元）

  • 公式： ReLU(x)=max(0,x) ReLU(x) = max(0, x)
  • 图像：左半轴恒为 0，右半轴恒为线性。（如下所示）

relu

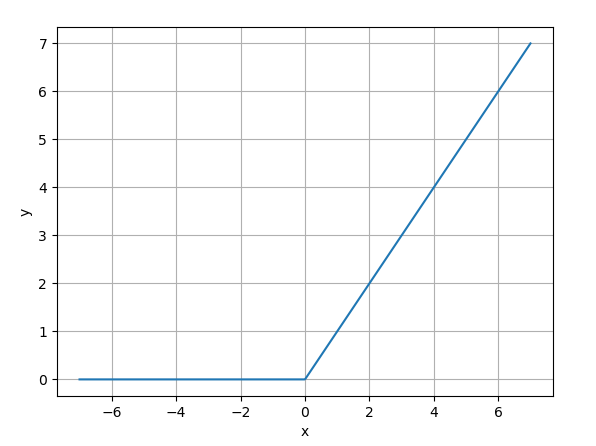
  • 优点：
    • 计算高效：无指数运算。
    • 缓解梯度消失：正区间导数为 1 。
  • 缺点：
    • Dead ReLU 问题：输入为负时梯度为 0，神经元”死亡“。
    • 输出非零中心化：
  • 适用场景：大多数前馈神经网络的隐藏层（默认选择）。

前馈神经网络（Feedforward Neural Network, FNN）是人工神经网络中最基础、最广泛使用的类型之一，其核心是数据单向流动（从输入层到输出层），没有循环或反馈连接。

5. Leaky ReLU

ReLU 的升级版

  • 公式： LeakyReLU(x)={x if x>0αx otherwiseLeakyReLU(x) = \left\{\begin{matrix} x \text{ if x>0} \\ \alpha x \text{ otherwise} \end{matrix}\right. （通常 α=0.01\alpha = 0.01）

  • 图像：（如下所示）

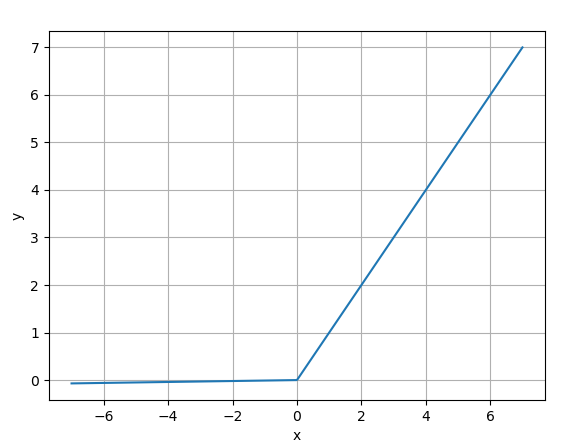
leaky_relu

  • 改进：负区间引入小斜率 α\alpha，缓解 Dead ReLU。
  • 优点：
    • 保留 ReLU 优点，减少神经元死亡。
  • 缺点：
    • α\alpha 需手动设定或学习。
  • 适用场景：需解决 Dead ReLU 问题的深层网络。

6. Parametric ReLU（PReLU）

Leaky ReLU 的升级版

  • 公式：类似于 Leaky ReLU，但 α\alpha 是可学习参数
  • 优点：自适应调整负区间斜率。
  • 缺点：增加参数量，可能过拟合。
  • 适用场景：大型网路（如 ResNet）

7. ELU（Exponential Linear Unit）

ReLU 的另一个升级版

  • 公式： ELU(x)={x if x>0α(ex−1)otherwiseELU(x) = \left\{\begin{matrix} x \text{ if x>0} \\ \alpha(e^x - 1) \text{otherwise} \end{matrix}\right.

  • 图像：（如下所示）

elu

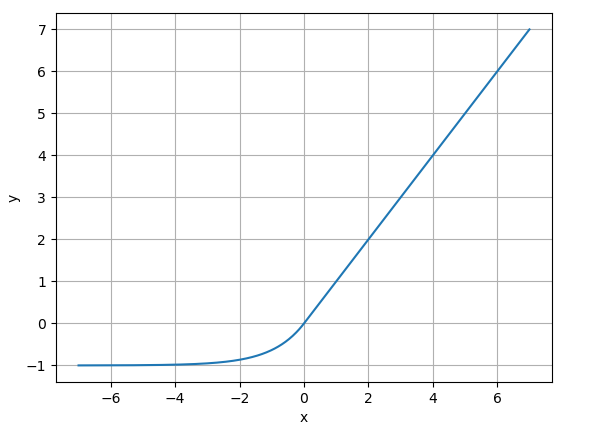
（通常 α=1\alpha = 1）

  • 优点：
    • 负区间平滑过渡，接近零均值输出。
    • 缓解 Dead ReLU 问题。
  • 缺点：
    • 指数计算增加复杂度。
  • 适用场景：深层网络，对噪声敏感的任务

8. Softmax

  • 公式： Softmax(xi)=exiΣj=1nexjSoftmax(x_i) = \frac{e^{x_i}}{\Sigma^n_{j=1} e^{x_j}}

  • 特点：将输出压缩为概率分布（总和为 1）。

  • 适用场景：多分类输出层。

9. Swish

  • 公式： Swish(x)=x⋅σ(βx)Swish(x) = x \cdot \sigma(\beta x) (σ\sigma 为 Sigmoid，β\beta 常设为 1 或可学习)

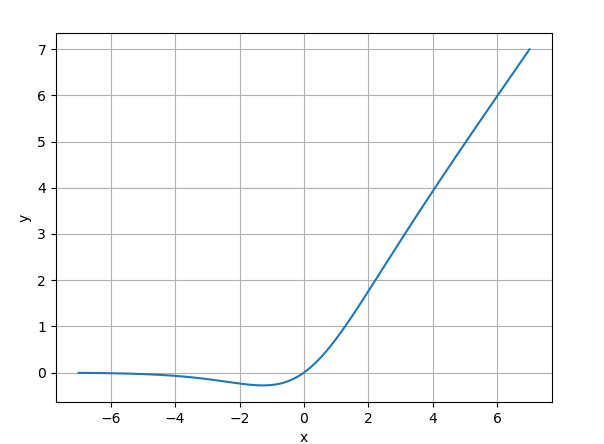
swish

  • 优点：
    • 平滑且非单调，实验显示优于 ReLU。
  • 缺点：计算量略大。
  • 适用场景：替代 ReLU 的隐藏层。

10. Mish

  • 公式： Mish(x)=x⋅tanh⁡(ln⁡(1+ex))Mish(x) = x \cdot \tanh(\ln(1+e^x))

mish

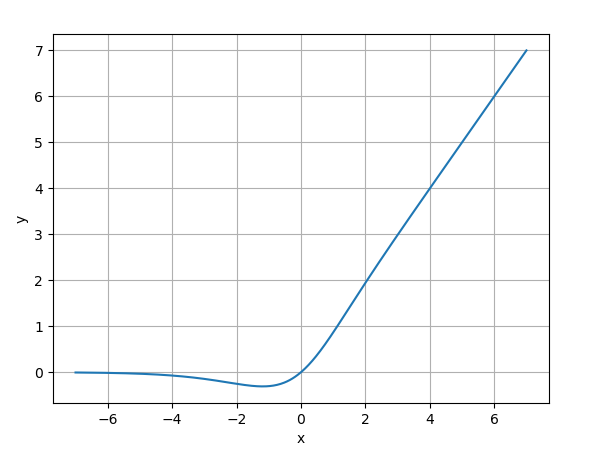
  • 优点：
    • 更平滑的梯度，缓解 Dead ReLU。
  • 缺点：计算成本高。
  • 适用场景：计算机视觉任务。